У математиці знаходження невідомого дільника є однією з ключових задач, пов’язаних із діленням і множенням. Цей процес допомагає розв’язувати рівняння, де один із компонентів дії ділення невідомий, і є важливим для учнів, які вивчають арифметику, а також для тих, хто застосовує математику в повсякденному житті. У цій статті ми розглянемо, як знайти невідомий дільник, які правила застосовуються для знаходження невідомих компонентів дій, як правильно завершити фразу “щоб знайти невідомий дільник”, а також надамо приклади для кращого розуміння.
Що таке дільник і чому важливо його знаходити?
У діленні є три основні компоненти:
- Ділене — число, яке ділять.
- Дільник — число, на яке ділять.
- Частка — результат ділення.

- 12 — ділене,
- 3 — дільник,
- 4 — частка.
Якщо один із компонентів, наприклад дільник, невідомий, ми можемо знайти його, використовуючи зв’язок між діленням і множенням, адже ділення є оберненим до множення. Знаходження невідомого дільника часто потрібне в задачах, рівняннях або для перевірки правильності обчислень.
Правила знаходження невідомого дільника
Щоб знайти невідомий дільник, потрібно скористатися основним правилом, яке випливає з взаємозв’язку між множенням і діленням. Ось ключові кроки та правила:
Основне правило: Щоб знайти невідомий дільник, треба ділене поділити на частку.

Зв’язок із множенням: Ділення можна представити як обернену операцію до множення.
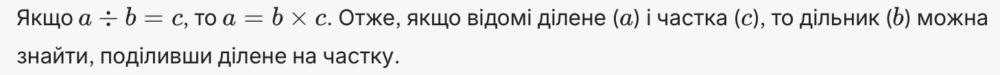
Перевірка: Після знаходження дільника перевірте правильність, підставивши його у вихідне рівняння або помноживши дільник на частку, щоб отримати ділене.
Умови: Частка не може дорівнювати нулю, оскільки ділення на нуль неможливе. Також результат ділення має бути цілим числом у випадках, коли задача стосується цілочисельного ділення.
Як знайти невідомий дільник: покроковий алгоритм
Щоб знайти невідомий дільник, виконайте такі кроки:
- Визначте відомі компоненти. З’ясуйте, які числа дані в задачі (ділене та частка).
- Застосуйте формулу. Поділіть ділене на частку, щоб знайти дільник.
- Перевірте результат. Помножте знайдений дільник на частку, щоб переконатися, що отримуєте вихідне ділене.
- Запишіть відповідь. Переконайтеся, що результат відповідає умовам задачі (наприклад, чи є дільник цілим числом).

Знаходження невідомого компонента дій множення
Оскільки ділення пов’язане з множенням, знаходження невідомого дільника аналогічне знаходженню одного з множників у множенні. Якщо у множенні a×b=c, і один із множників (b) невідомий, то:
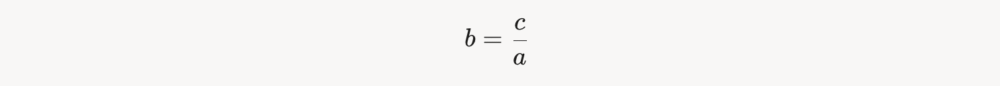
Це та сама логіка, що й у діленні, адже ділене відповідає добутку, а частка — одному з множників. Наприклад:

Таким чином, знаходження невідомого дільника чи множника базується на одній і тій самій формулі.
Як правильно завершити фразу: “Щоб знайти невідомий дільник…”
Фраза “Щоб знайти невідомий дільник…” найчастіше завершується так: “Щоб знайти невідомий дільник, треба ділене поділити на частку.” Ця фраза відображає основне правило і є лаконічною та зрозумілою. Наприклад:
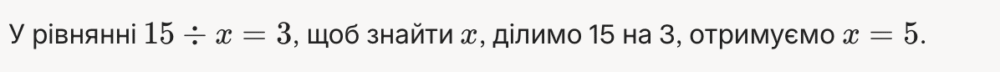
Практичні приклади для різних рівнів складності
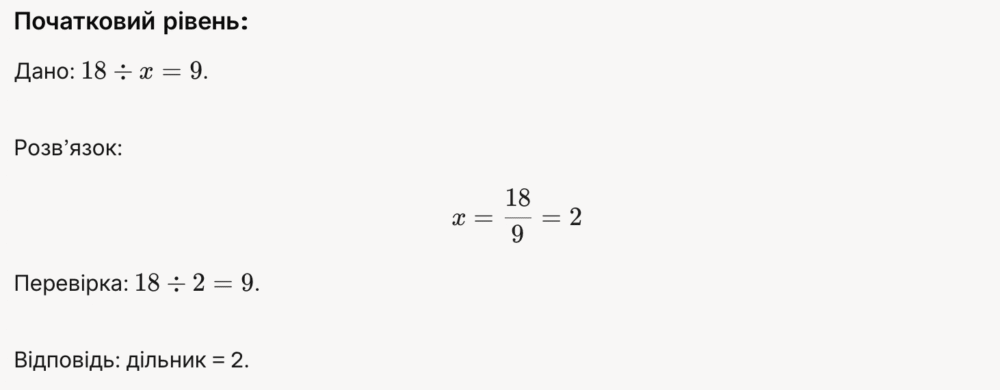

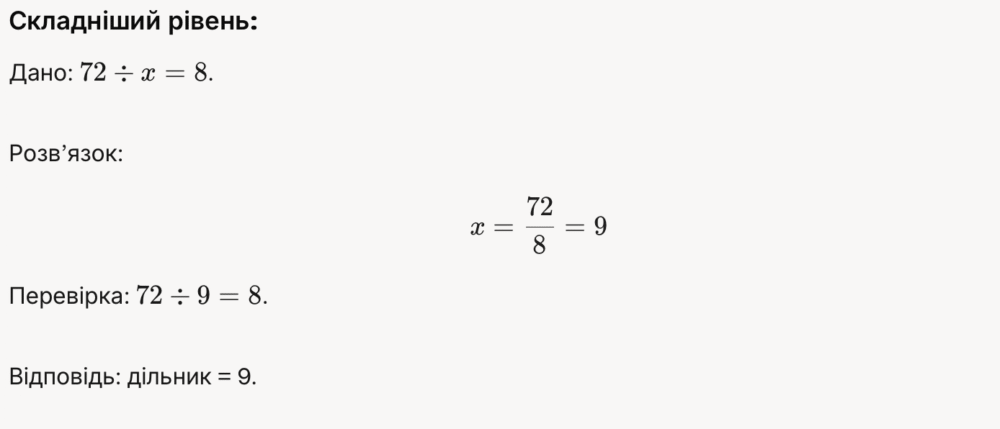
Поширені помилки та як їх уникнути
- Ділення на нуль. Якщо частка дорівнює нулю, дільник знайти неможливо, адже ділення на нуль не визначене. Переконайтеся, що частка не нуль.
- Неправильна перевірка. Завжди перевіряйте результат, підставляючи знайдений дільник у вихідне рівняння.
- Неврахування умов задачі. Якщо задача вимагає цілочисельного дільника.

Поради для учнів і вчителів
Використовуйте наочність. Для молодших школярів можна малювати схеми чи використовувати предмети (наприклад, яблука чи кубики), щоб пояснити ділення. Тренуйтеся на простих прикладах. Починайте з чисел, які легко діляться, наприклад, 12, 24, 30, щоб учні зрозуміли принцип.
Пов’язуйте з реальним життям. Задачі про розподіл цукерок, грошей чи часу роблять навчання цікавішим. Використовуйте множення для перевірки. Завжди нагадуйте учням, що дільник × частка = ділене.
Знаходження невідомого дільника — це проста, але важлива математична навичка, яка допомагає розв’язувати рівняння та задачі. Основне правило звучить так: щоб знайти невідомий дільник, треба ділене поділити на частку. Цей процес базується на зв’язку між діленням і множенням, що робить його універсальним для різних типів задач. Використовуйте наведені приклади, перевіряйте результати та тренуйтеся на задачах із реального життя, щоб опанувати цю навичку. Незалежно від того, чи ви учень, чи вчитель, розуміння, як знайти невідомий дільник, відкриває двері до глибшого розуміння математики та її практичного застосування.





